How To Fake Weight On Scale

Logic puzzle

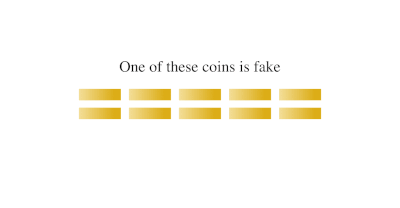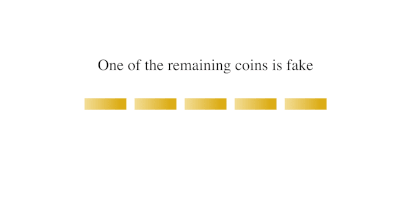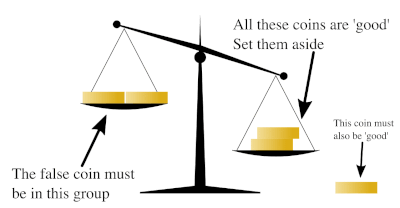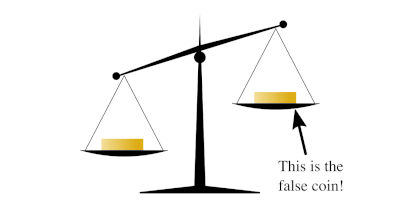
An animation of a solution to the a imitation coin problem involving ten coins. In this case, the fake coin is lighter than the others.

A balance puzzle or weighing puzzle is a logic puzzle about balancing items—frequently coins—to determine which holds a unlike value, past using balance scales a limited number of times. These differ from puzzles that assign weights to items, in that merely the relative mass of these items is relevant.

Known	Goal	Maximum Coins for northward weighings	Number of Weighings for c coins
Whether target coin is lighter or heavier than others	Identify coin	${\displaystyle three^{northward}}$	${\displaystyle \lceil \log _{3}(c)\rceil }$
Target coin is unlike from others	Identify coin	${\displaystyle {\frac {3^{n}-1}{2}}}$ [1]	${\displaystyle \lceil \log _{3}(2c+1)\rceil }$
Target coin is unlike from others, or all coins are the aforementioned	Place if unique coin exists, and whether it is lighter or heavier	${\displaystyle {\frac {3^{n}-ane}{two}}-one}$	${\displaystyle \lceil \log _{iii}(2c+3)\rceil }$

For case, in detecting a dissimilar money in three weighings (n = three), the maximum number of coins that can exist analyzed is 3ⁱⁱⁱ − 1 / 2 = 13. Note that with 3 weighs and 13 coins, it is non always possible to determine the identity of the last money (whether it is heavier or lighter than the residuum), simply only that the coin is different. In full general, with n weighs, you lot tin determine the identity of a coin if you have three ⁿ − ane / 2 - one or less coins. In the example n = iii, you can truly discover the identity of the different coin out of 12 coins.

Ix-coin trouble [edit]

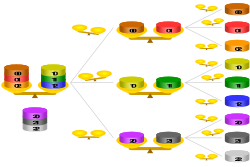
Solution to the balance puzzle for 9 coins in 2 weighings, where the odd coin is lighter than the others – if the odd coin were heavier than the others, the upper 2 branches in each weighing decision are swapped

A well-known example has up to nine items, say coins (or balls), that are identical in weight except ane, which is lighter than the others—a apocryphal (an oddball). The difference is perceptible only by weighing them on scale—only only the coins themselves can be weighed. How tin i isolate the counterfeit coin with only two weighings?

Solution [edit]

To find a solution, nosotros beginning consider the maximum number of items from which one tin can find the lighter one in but ane weighing. The maximum number possible is three. To find the lighter i, nosotros can compare whatever two coins, leaving the third out. If the two coins counterbalance the same, so the lighter coin must be 1 of those not on the remainder. Otherwise, information technology is the one indicated as lighter past the rest.

At present, imagine the nine coins in three stacks of three coins each. In one move we can find which of the three stacks is lighter (i.eastward. the 1 containing the lighter coin). It so takes merely one more than move to identify the light coin from within that lighter stack. And then in two weighings, we can find a unmarried calorie-free coin from a set of iii × 3 = 9.

By extension, information technology would take only three weighings to find the odd light coin amongst 27 coins, and four weighings to observe it from 81 coins.

Twelve-money problem [edit]

A more than circuitous version has twelve coins, eleven or twelve of which are identical. If i is different, nosotros don't know whether information technology is heavier or lighter than the others. This time the balance may be used three times to decide if there is a unique coin—and if there is, to isolate information technology and determine its weight relative to the others. (This puzzle and its solution start appeared in an article in 1945.^[two]) The problem has a simpler variant with 3 coins in 2 weighings, and a more than complex variant with 39 coins in iv weighings.

Solution [edit]

This problem has more than than i solution. One is hands scalable to a higher number of coins by using base-three numbering: labeling each coin with a different number of three digits in base of operations iii, and positioning at the n-th weighings all the coins that are labeled with the n-th digit identical to the label of the plate (with three plates, 1 on each side of the scale and ane off the scale). Other footstep-by-step procedures are like to the following. It is less straightforward for this problem, and the second and 3rd weighings depend on what has happened previously, although that need not be the case (see below).

• Four coins are put on each side. In that location are two possibilities:

i. One side is heavier than the other. If this is the case, remove three coins from the heavier side, move three coins from the lighter side to the heavier side, and place three coins that were non weighed the first time on the lighter side. (Think which coins are which.) In that location are three possibilities:

1.a) The same side that was heavier the first fourth dimension is still heavier. This means that either the money that stayed in that location is heavier or that the coin that stayed on the lighter side is lighter. Balancing ane of these against one of the other ten coins reveals which of these is truthful, thus solving the puzzle.

1.b) The side that was heavier the first time is lighter the second time. This means that one of the three coins that went from the lighter side to the heavier side is the light coin. For the third endeavour, weigh two of these coins against each other: if 1 is lighter, it is the unique coin; if they balance, the third money is the light one.

1.c) Both sides are even. This means that one of the three coins that was removed from the heavier side is the heavy money. For the third try, weigh two of these coins against each other: if one is heavier, it is the unique coin; if they balance, the third coin is the heavy one.

2. Both sides are even. If this is the case, all eight coins are identical and can be prepare aside. Accept the four remaining coins and place iii on 1 side of the rest. Place 3 of the viii identical coins on the other side. There are three possibilities:

2.a) The 3 remaining coins are lighter. In this case you at present know that ane of those three coins is the odd one out and that information technology is lighter. Accept two of those three coins and weigh them against each other. If the remainder tips so the lighter coin is the odd one out. If the 2 coins rest then the third coin non on the residual is the odd one out and information technology is lighter.

2.b) The three remaining coins are heavier. In this case you at present know that 1 of those iii coins is the odd one out and that it is heavier. Take two of those three coins and counterbalance them confronting each other. If the balance tips and so the heavier coin is the odd one out. If the two coins balance so the 3rd coin not on the balance is the odd one out and it is heavier.

2.c) The 3 remaining coins balance. In this instance you merely need to weigh the remaining coin against whatever of the other eleven coins and this tells you lot whether it is heavier, lighter, or the same.

Variations [edit]

Given a population of 13 coins in which it is known that i of the 13 is different (mass) from the residue, it is elementary to determine which coin information technology is with a balance and iii tests as follows:

ane) Subdivide the coins in to ii groups of 4 coins and a third grouping with the remaining 5 coins.

2) Test 1, Test the 2 groups of 4 coins confronting each other:

a. If the coins balance, the odd money is in the population of v and go along to test 2a.

b. The odd coin is among the population of 8 coins, continue in the same style as in the 12 coins problem.

3) Test 2a, Test 3 of the coins from the group of 5 coins confronting whatever three coins from the population of 8 coins:

a. If the three coins balance, then the odd money is amid the remaining population of ii coins. Test i of the ii coins against whatever other coin; if they balance, the odd coin is the last untested money, if they do not balance, the odd coin is the electric current test money.

b. If the 3 coins do non residuum, then the odd money is from this population of iii coins. Pay attention to the direction of the balance swing (upwards means the odd coin is calorie-free, down means it is heavy). Remove one of the 3 coins, move another to the other side of the remainder (remove all other coins from residual). If the balance evens out, the odd money is the money that was removed. If the residue switches direction, the odd coin is the one that was moved to the other side, otherwise, the odd coin is the coin that remained in place.

With a reference money [edit]

If there is one authentic money for reference then the suspect coins can be thirteen. Number the coins from ane to xiii and the authentic coin number 0 and perform these weighings in any order:

• 0, 1, four, 5, 6 against 7, 10, eleven, 12, xiii
• 0, 2, iv, 10, xi confronting 5, 8, 9, 12, 13
• 0, 3, 8, 10, 12 against 6, 7, 9, 11, 13

If the scales are only off residuum once, then information technology must exist one of the coins 1, 2, 3—which only appear in one weighing. If there is never residuum then it must be one of the coins 10–xiii that appear in all weighings. Picking out the one counterfeit coin corresponding to each of the 27 outcomes is always possible (xiii coins one either too heavy or too light is 26 possibilities) except when all weighings are balanced, in which example there is no counterfeit coin (or its weight is correct). If coins 0 and 13 are deleted from these weighings they give 1 generic solution to the 12-coin problem.

If two coins are counterfeit, this procedure, in general, does not pick either of these, just rather some authentic coin. For example, if both coins 1 and 2 are counterfeit, either coin four or v is wrongly picked.

Without a reference coin [edit]

In a relaxed variation of this puzzle, one only needs to discover the apocryphal coin without necessarily existence able to tell its weight relative to the others. In this instance, clearly whatsoever solution that previously weighed every money at some betoken tin can be adapted to handle one extra coin. This money is never put on the scales, but if all weighings are counterbalanced it is picked every bit the counterfeit coin. It is not possible to do any better, since any money that is put on the scales at some point and picked as the counterfeit coin can and so always exist assigned weight relative to the others.

A method which weighs the aforementioned sets of coins regardless of outcomes lets i either

1. (amongst 12 coins A–Fifty) conclude if they all weigh the same, or find the odd coin and tell if it is lighter or heavier, or
2. (among 13 coins A–M) find the odd coin, and, at 12/13 probability, tell if it is lighter or heavier (for the remaining 1/13 probability, merely that it is dissimilar).

The three possible outcomes of each weighing can be denoted by "\" for the left side existence lighter, "/" for the correct side existence lighter, and "–" for both sides having the same weight. The symbols for the weighings are listed in sequence. For example, "//–" means that the right side is lighter in the first and 2d weighings, and both sides weigh the same in the 3rd weighing. Three weighings give the following three³ = 27 outcomes. Except for "–––", the sets are divided such that each attack the correct has a "/" where the set up on the left has a "\", and vice versa:

/// \\\  \// /\\ /\/ \/\ //\ \\/  \/– /\– –\/ –/\ /–\ \–/  \\– //– –\\ –// \–\ /–/  /–– \–– –/– –\– ––/ ––\  –––        

Equally each weighing gives a meaningful upshot simply when the number of coins on the left side is equal to the number on the correct side, we disregard the first row, so that each cavalcade has the aforementioned number of "\" and "/" symbols (four of each). The rows are labelled, the social club of the coins being irrelevant:

\// A light    /\\ A heavy /\/ B light    \/\ B heavy //\ C lite    \\/ C heavy  \/– D light    /\– D heavy –\/ E light    –/\ E heavy /–\ F light    \–/ F heavy  \\– G light    //– G heavy –\\ H low-cal    –// H heavy \–\ I light    /–/ I heavy  /–– J light    \–– J heavy –/– K light    –\– K heavy ––/ L light    ––\ L heavy  ––– Thou either lighter or heavier (13-coin case),     or all coins weigh the same (12-money case)        

Using the pattern of outcomes higher up, the composition of coins for each weighing tin exist adamant; for example the set "\/– D light" implies that coin D must be on the left side in the showtime weighing (to cause that side to be lighter), on the right side in the second, and unused in the tertiary:

1st weighing:  left side: ADGI, right side: BCFJ 2nd weighing:  left side: BEGH, right side: ACDK tertiary weighing:  left side: CFHI, right side: ABEL        

The outcomes are so read off the table. For example, if the correct side is lighter in the first 2 weighings and both sides weigh the aforementioned in the 3rd, the respective code "//– One thousand heavy" implies that coin Chiliad is the odd 1, and it is heavier than the others.^[3]

Generalizations [edit]

The generalization of this problem is described in Chudnov.^[4]

Let ${\displaystyle \mathbb {R} ^{north}}$ be the ${\displaystyle northward}$ -dimensional Euclidean space, ${\displaystyle [\mathrm {e} ^{one},\mathrm {e} ^{ii}]}$ exist the inner product of vectors ${\displaystyle \mathrm {due east} ^{1}}$ and ${\displaystyle \mathrm {e} ^{two}}$ from ${\displaystyle \mathbb {R} ^{n},}$ For vectors ${\displaystyle \mathrm {e} =(e_{1},\dots ,e_{north})\in \mathbb {R} ^{n}}$ and subsets ${\displaystyle Due east=\{\mathrm {e} ^{j}\}\subseteq \mathbb {R} ^{n},}$ the operations ${\displaystyle (\cdot )^{*}}$ and ${\displaystyle (\cdot )^{+}}$ are defined, respectively, equally ${\displaystyle \mathrm {e} ^{*}=(sign(e_{i}))_{i}}$  ; ${\displaystyle East^{*}=\{(\mathrm {eastward} ^{j})^{*}\}}$ , ${\displaystyle \mathrm {east} ^{+}=(|sign(e_{i})|)_{i}}$ , ${\displaystyle Eastward^{+}=\{(\mathrm {e} ^{j})^{+}\}.}$ By ${\displaystyle I^{n}}$ we shall denote the discrete [−i; 1]-cube in ${\displaystyle \mathbb {R} ^{n}}$ ; i.east., the set up of all sequences of length ${\displaystyle n}$ over the alphabet ${\displaystyle I=\{-ane,0,1\}}$ The set ${\displaystyle I_{t}^{n}=\{\mathrm {x} \in I^{n}|w(\mathrm {ten} )\leq t\}\subseteq I^{n}}$ is the discrete ball of radius ${\displaystyle t}$ (in the Hamming metric ${\displaystyle west()}$ ) with center at the point ${\displaystyle \mathrm {0} .}$ Relative weights of ${\displaystyle n}$ objects are given past a vector ${\displaystyle \mathrm {x} =(x_{1},\dots ,x_{n})\in I^{north},}$ which defines the configurations of weights of the objects: the ${\displaystyle i}$ th object has standard weight if ${\displaystyle x_{i}=0;}$ the weight of the ${\displaystyle i}$ th object is greater (smaller) by a abiding (unknown) value if ${\displaystyle x_{i}=ane}$ (respectively, ${\displaystyle x_{i}=-1}$ ). The vector ${\displaystyle \mathrm {x} ^{+}}$ characterizes the types of objects: the standard blazon, the non-standard type (i.e., configurations of types), and it does not contain information about relative weights of non-standard objects.

A weighing (a check) is given by a vector ${\displaystyle \mathrm {h} \in I^{n};}$ the event of a weighing for a situation ${\displaystyle \mathrm {x} \in I^{n}}$ is ${\displaystyle s(\mathrm {x} ;\mathrm {h} )=sign([\mathrm {x} ;\mathrm {h} ]).}$ The weighing given by a vector ${\displaystyle \mathrm {h} =(h_{1},\dots ,h_{n})}$ has the following estimation: for a given check the ${\displaystyle i}$ th object participates in the weighing if ${\displaystyle h_{i}\neq 0}$ ; it is put on the left balance pan if ${\displaystyle h_{i}<0}$ and is put on the right pan if ${\displaystyle h_{i}>0.}$ For each weighing ${\displaystyle \mathrm {h} }$ , both pans should incorporate the same number of objects: if on some pan the number of objects is smaller than as it should be, and then it receives some ${\displaystyle r(\mathrm {h} )=[\mathrm {h} ;1,\dots ,1]}$ reference objects. The result of a weighing ${\displaystyle due south(\mathrm {ten} ;\mathrm {h} )}$ describes the following cases: the rest if ${\displaystyle south(\mathrm {x} ;\mathrm {h} )=0}$ , the left pan outweighs the right one if ${\displaystyle s(\mathrm {10} ;\mathrm {h} )=-ane}$ , and the right pan outweighs the left one if ${\displaystyle southward(\mathrm {ten} ;\mathrm {h} )=one.}$ The incompleteness of initial information nigh the distribution of weights of a group of objects is characterized by the set up of open-door distributions of weights of objects ${\displaystyle Z\subseteq I^{n},}$ which is too called the ready of admissible situations, the elements of ${\displaystyle z\in Z}$ are called admissible situations.

Each weighing ${\displaystyle \mathrm {h} }$ induces the segmentation of the set ${\displaystyle I^{n}}$ past the plane (hyperplane ) ${\displaystyle [\mathrm {x} ;\mathrm {h} ]=0}$ into 3 parts ${\displaystyle Westward(s|I^{northward};\mathrm {h} )=\{\mathrm {x} \in I^{northward}|s(\mathrm {x} ;\mathrm {h} )=s\}}$ , ${\displaystyle s\in I,}$ and defines the respective partition of the set ${\displaystyle Z=W(0|Z,\mathrm {h} )+Westward(1|Z,\mathrm {h} )+W(-ane|Z,\mathrm {h} ),}$ where ${\displaystyle W(s|Z,\mathrm {h} )=West(due south|I^{n},\mathrm {h} )\cap Z.}$

Definition 1. A weighing algorithm (WA) ${\displaystyle {\mathcal {A}}}$ of length ${\displaystyle m}$ is a sequence ${\displaystyle {\mathcal {A}}=<\mathrm {A} _{i},\dots ,\mathrm {A} _{m}>,}$ where ${\displaystyle \mathrm {A} _{j}:I^{j-i}\to I^{n}}$ is the function determining the check ${\displaystyle \mathrm {h} ^{j}=\mathrm {A} _{j}(s^{j-1});\mathrm {h} ^{j}\in I^{n},}$ at each ${\displaystyle j}$ th step, ${\displaystyle j=1,ii,\dots ,thousand,}$ of the algorithm from the results of ${\displaystyle \mathrm {southward} ^{j-one}=(s_{1},\dots ,s_{j-1})\in I^{j-1}}$ weighings at the previous steps ( ${\displaystyle \mathrm {h} ^{one}=\mathrm {A} _{one}()}$ is a given initial check).

Let ${\displaystyle South(Z,{\mathcal {A}})}$ exist the set of all ${\displaystyle (Z,{\mathcal {A}})}$ -syndromes and ${\displaystyle West(southward|{\mathcal {A}})\subseteq I}$ be the fix of situations with the same syndrome ${\displaystyle s}$ ; i.east., ${\displaystyle Westward(due south|{\mathcal {A}})=\{\mathrm {z} \in I^{1000}|s(z|{\mathcal {A}})=s\}}$ ; ${\displaystyle W(south|Z;{\mathcal {A}})=W(s|{\mathcal {A}})\cap Z.}$

Definition 2. A WA ${\displaystyle {\mathcal {A}}}$ is said to: a) identify the situations in a prepare ${\displaystyle Z}$ if the condition ${\displaystyle |W(s|Z,{\mathcal {A}})|=1}$ is satisfied for all ${\displaystyle s\in Southward(Z{\mathcal {A}});}$ b) identify the types of objects in a prepare ${\displaystyle Z}$ if the condition ${\displaystyle |West^{+}(south|Z{\mathcal {A}})|=1}$ is satisfied for all ${\displaystyle s\in Southward(Z{\mathcal {A}}).}$

It is proved in ^[iv] that for so-chosen suitable sets ${\displaystyle Z}$ an algorithm of identification the types identifies too the situations in ${\displaystyle Z.}$

As an instance the perfect dynamic (two-pour) algorithms with parameters ${\displaystyle due north=xi,m=5,t=ii}$ are synthetic in ^[iv] which represent to the parameters of the perfect ternary Golay code (Virtakallio-Golay code). At the same fourth dimension, information technology is established that a static WA (i.e. weighting code) with the same parameters does not exist.

Each of these algorithms using 5 weighings finds amongst 11 coins upward to two counterfeit coins which could be heavier or lighter than real coins by the same value. In this case the uncertainty domain (the set of admissible situations) contains ${\displaystyle ane+2C_{11}^{ane}+2^{ii}C_{11}^{2}=iii^{5}}$ situations, i.due east. the constructed WA lies on the Hamming jump for ${\displaystyle t=2}$ and in this sense is perfect.

To appointment information technology is not known whether there are other perfect WA that identify the situations in ${\displaystyle I_{t}^{north}}$ for some values of ${\displaystyle n,t}$ . Moreover, it is not known whether for some ${\displaystyle t>2}$ there exist solutions for the equation ${\displaystyle \sum _{i=0}^{t}2^{i}C_{due north}^{i}=3^{chiliad}}$ (corresponding to the Hamming jump for ternary codes) which is, obviously, necessary for the existence of a perfect WA. It is only known that for ${\displaystyle t=1}$ in that location are no perfect WA, and for ${\displaystyle t=2}$ this equation has the unique nontrivial solution ${\displaystyle due north=11,thousand=5}$ which determines the parameters of the constructed perfect WA.

Original parallel weighings puzzle [edit]

Eliran Sabag invented this puzzle{1https://www.youtube.com/watch?five=y7auJNBA0bs}. At that place are North indistinguishable coins, one of which is imitation (it is non known whether it is heavier or lighter than the 18-carat coins, which all weigh the same). At that place are ii residuum scales that tin can be used in parallel. Each weighing lasts three minute. What is the largest number of coins N for which it is possible to find the fake coin in ten minutes?^[5]

In literature [edit]

• Niobe, the protagonist of Piers Anthony's novel With a Tangled Skein, must solve the twelve-coin variation of this puzzle to observe her son in Hell: Satan has disguised the son to look identical to eleven other demons, and he is heavier or lighter depending on whether he is cursed to lie or able to speak truthfully. The solution in the book follows the given instance one.c.
• Beremiz, the master character from Júlio César de Mello eastward Souza'south book The Human Who Counted, encounters an Indian merchant that challenges him with the standard residue puzzle with eight identical-shaped pearls (one pearl slightly lighter than the rest). Beremiz solves it by explicitly framing all the variables of the problem, using only ii weighings.

In tv [edit]

• In the episode "The Wedding Scammer" of Cyberchase, the group of protagonists must detect a lighter key out of eight keys (the other seven weigh the same), and they solve it suboptimally, with three weightings, when two suffices.
• In the episode "The Bye-Bye Sky High IQ Murder Case" of Columbo, Columbo solves the following puzzle: https://world wide web.mathsisfun.com/puzzles/weighing-x-bags-solution.html
• In the episode "Captain Peralta" of Brooklyn Nine-Nine, Holt presents to his squad a version of the twelve-coin problem involving twelve men and a seesaw.

References [edit]

1. ^ Weisstein, Eric W. "Weighing". mathworld.Wolfram.com . Retrieved 16 Baronial 2017.
2. ^ Grossman, Howard (1945). Scripta Mathematica 11.
3. ^ "Math Forum - Enquire Dr. Math". mathforum.org. Archived from the original on 2002-06-12.
4. ^ ^{a b c} Chudnov, Alexander Chiliad. (2015). "Weighing algorithms of classification and identification of situations". Discrete Mathematics and Applications. 25 (2): 69–81. doi:x.1515/dma-2015-0007. S2CID 124796871.
5. ^ Khovanova, Tanya (2013). "Solution to the Counterfeit Coin Problem and its Generalization". arXiv:1310.7268 [math.HO].

External links [edit]

• A playable example of the 2d puzzle
• 2-pan remainder and generalized counterfeit coin trouble

Source: https://en.wikipedia.org/wiki/Balance_puzzle

Share this post